
- Autor Stanley Ellington [email protected].
- Public 2023-12-16 00:17.
- Zadnja promjena 2025-01-22 16:00.
Ova stranica navodi dokaze za Eulerova formula : za bilo koji konveksni poliedar, the broj od vrhovima i lica zajedno je točno dva više od broj od rubovi . Simbolično V−E+F=2. Za primjer, a tetraedar ima četiri vrha , četiri lica , i šest rubovi ; 4 - 6 + 4 =2.
Posljedično, koliki će biti broj lica ako ima 6 vrhova i 12 bridova?
Kocka ili kvadar je trodimenzionalni oblik koji ima 12 rubova , 8 uglovima ili vrhovima , i 6 lica.
Također se može zapitati kako funkcionira Eulerova formula? Eulerova formula , Bilo koji od dva važna matematička teorema Leonharda Euler . Prvi je topološka invarijantnost (vidi topologiju) koja se odnosi na broj lica, vrhova i bridova bilo kojeg poliedra. Piše se F + V = E + 2, gdje je F broj lica, V broj vrhova, a E broj bridova.
koja je formula za odnos između broja vrhova lica i bridova kocke?
V - E + F = 2; ili, riječima: the broj od vrhovima , minus broj od rubovi , plus broj lica , je jednako do dva.
Što je Eulerova formula poliedra?
Ovaj teorem uključuje Eulerova poliedarska formula (ponekad se zove Eulerova formula ). Danas bismo ovaj rezultat naveli kao: Broj vrhova V, lica F i bridova E u konveksnoj 3-dimenzionalnoj poliedar , zadovoljavaju V + F - E = 2.
Preporučeni:
Je li serijski broj isti kao i VIN broj na mobilnoj kućici?

1) U unutrašnjosti svih mobilnih kućica proizvedenih od lipnja 1976. nalazi se papirnata naljepnica, nazvana "tablica s podacima", koja navodi VIN broj (koji se naziva i serijski broj), zajedno s drugim činjenicama o proizvodnji doma . VIN će se zvati serijski broj proizvođača na pločici s podacima
Koja su tri načina na koja Fbla koristi studentima?

Ispod je 6 prednosti pridruživanja FBLA. Cilj mu je razviti buduće lidere. Nudi programe stipendiranja. Otvara jedinstvena vrata mogućnosti. Uči vas što je važno. Omogućuje vam ekskluzivne popuste i dodatne pogodnosti. To te čini boljom osobom
Što je P broj i broj grupe?

Obični metali: P broj Ovaj se broj koristi za grupiranje sličnih osnovnih metala, omogućujući kvalifikaciju cijelog odabira u odnosu na kvalifikaciju samo jednog. Ovi osnovni metali su grupirani prema materijalu i dodijeljeni su P brojevima na temelju materijala koji su
Koja je kultura zapošljavala najveći broj robova na jednoj plantaži?

Na donjem jugu većina robova živjela je i radila na plantažama pamuka. Većina tih plantaža imala je pedesetak ili manje robova, iako najveće plantaže imaju nekoliko stotina. Pamuk je bio daleko vodeći usjev, ali robovi su također uzgajali rižu, kukuruz, šećernu trsku i duhan
Kako pomnožiti mješoviti broj puta cijeli broj?
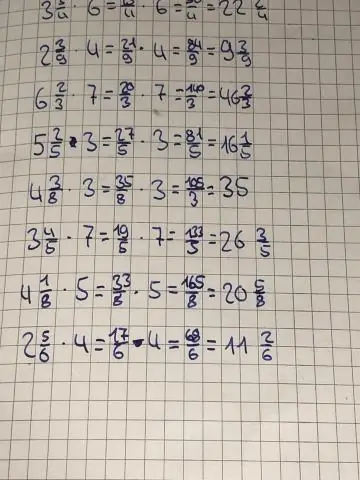
Množenje mješovitog broja i cijelog broja Mješoviti broj se pretvara u nepravilan razlomak i cijeli se broj zapisuje kao razlomak s nazivnikom. Provodi se množenje razlomaka i po potrebi pojednostavljivanje. Rezultirajući razlomak zapisuje se kao najjednostavniji oblik mješovitog broja
