
- Autor Stanley Ellington [email protected].
- Public 2023-12-16 00:17.
- Zadnja promjena 2025-01-22 16:00.
A normalna distribucija ima zvonastu krivulju i simetrično je oko središta, tako da je desna strana središta zrcalna slika lijeve strane. Većina kontinuiranih vrijednosti podataka u a normalna distribucija imaju tendenciju grupiranja oko srednje vrijednosti, a što je vrijednost dalje od srednje vrijednosti, manja je vjerojatnost da će se pojaviti upala.
Prema tome, što je normalna distribucija u statistici definicija?
A normalna distribucija je raspored skupa podataka u kojem se većina vrijednosti grupira u sredini rasponu a ostatak se sužava simetrično prema bilo kojoj krajnosti. Precizni oblik može varirati ovisno o distribucija stanovništva, ali vrh je uvijek u sredini i krivulja je uvijek simetrična.
Također se može zapitati što je savršena normalna distribucija? Od " savršen " normalna distribucija gotovo se nikada ne pojavljuje u podacima iz stvarnog svijeta (gdje " savršen " normalna distribucija definira se kao 1. the distribucija je savršeno simetrično između svih standardnih devijacija na obje strane srednje vrijednosti i 3.
Također znate, koja su svojstva normalne distribucije u statistici?
Karakteristike normalne distribucije Normalne distribucije su simetrični, unimodalni i asimptotični, a srednja vrijednost, medijan i mod su jednaki. A normalna distribucija savršeno je simetričan oko središta. To jest, desna strana središta je zrcalna slika lijeve strane.
Koja je normalna distribucija vjerojatnosti?
Vjerojatnost i Normalna krivulja The normalna distribucija je kontinuirano raspodjela vjerojatnosti . Ovo ima nekoliko implikacija za vjerojatnost . Ukupna površina ispod normalna krivulja jednako 1. The vjerojatnost da je normalan slučajna varijabla X jednaka je bilo kojoj određenoj vrijednosti is0.
Preporučeni:
Što pokazuje normalna krivulja distribucije?

Krivulja normalne distribucije. U statistici, teoretska krivulja koja pokazuje koliko često će eksperiment dati određeni rezultat. Krivulja je simetrična i zvonastog oblika, što pokazuje da će pokusi obično dati rezultat blizu prosjeka, ali će povremeno odstupati za velike količine
Što je distribucija u marketing mixu?
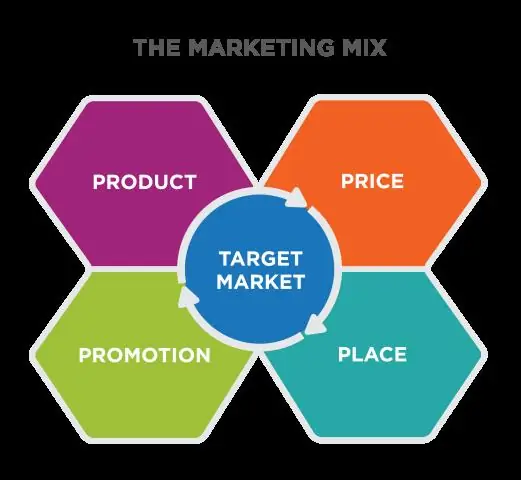
Distribucija (ili mjesto) jedan je od četiri elementa marketinškog miksa. Distribucija je proces stavljanja proizvoda ili usluge na raspolaganje potrošaču ili poslovnom korisniku koji ga treba. To može učiniti izravno proizvođač ili pružatelj usluga ili korištenjem neizravnih kanala s distributerima ili posrednicima
Što je zbirna distribucija?
Ovaj Zakon predviđa način da se osobna imovina umrle osobe, sudskim postupkom, podijeli po skraćenom načinu raspodjele preživjelom supružniku ili odgovarajuća podjela ostavitelja, bez pune ostavinske uprave
Što je normalna potreba?

U ekonomiji, nužno dobro ili nužno dobro je vrsta normalnog dobra. Kao i za bilo koje drugo normalno dobro, porast dohotka će dovesti do porasta potražnje, ali povećanje za nužnu robu je manje nego proporcionalno porastu dohotka, tako da udio rashoda na ta dobra opada kako dohodak raste
Što je distribucija usluga?

Distribucija je proces stavljanja proizvoda ili usluge na raspolaganje potrošaču ili poslovnom korisniku koji ga treba. To može učiniti izravno proizvođač ili pružatelj usluga ili korištenjem neizravnih kanala s distributerima ili posrednicima. Cjelokupni distribucijski kanal trebao bi dodati vrijednost potrošaču
